
Imagina las compuertas lógicas como los bloques de construcción de los circuitos digitales, que al combinarse permiten crear sistemas tan sofisticados como computadoras, smartphones y dispositivos IoT. Estos circuitos se forman con componentes esenciales como transistores NPN y PNP, resistencias y diodos, organizados para procesar señales binarias (0 y 1).
Al unir compuertas lógicas (como AND y OR), se pueden desarrollar funciones avanzadas que controlan el flujo de corriente de manera precisa y modular. Este enfoque es ideal para proyectos DIY, experimentos en protoboards o simulaciones en plataformas como Tinkercad, abriendo las puertas a la innovación en electrónica y tecnología digital.
A continuación, te presentamos un ejemplo práctico en Tinkercad. En esta simulación verás cómo se implementa una compuerta AND utilizando transistores, lo que te permitirá observar de manera directa el funcionamiento de estos bloques esenciales en un circuito digital. Ejecuta la simulación y experimenta por ti mismo la integración de componentes en un proyecto DIY de electrónica.
El proyecto para hacer una compuerta lógica AND con transistores es muy sencillo:
2x Protoboard 400 puntos o similar
2 x Interruptor dip switch o similar
1 x LED luminoso
Fuente de alimentación 5V para protoboard o batería de 9V con broche de conexión
Tipos de Compuertas Lógicas y Sus Símbolos
Existen 7 compuertas lógicas básicas – cada una con una función única en el álgebra booleana – que puedes ver como las “herramientas” fundamentales en la creación de circuitos lógicos. Aquí te mostramos sus características principales y símbolos estándar (según ANSI/IEEE):
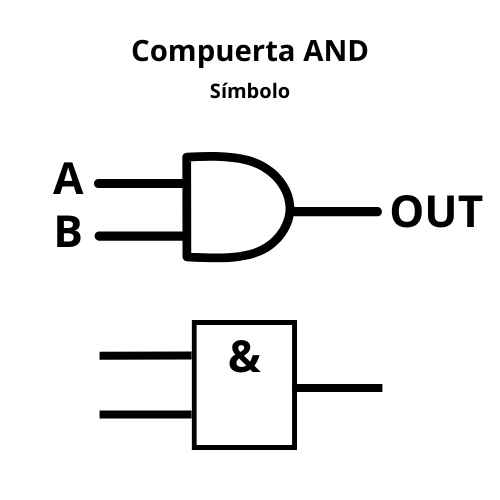
- AND (Y)
- Función: La salida es 1 solo si todas las entradas son 1.
- Símbolo: Rectángulo con un “&” interno.
- Tabla de verdad compuerta lógica AND
| Entrada A | Entrada B | Salida (A AND B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
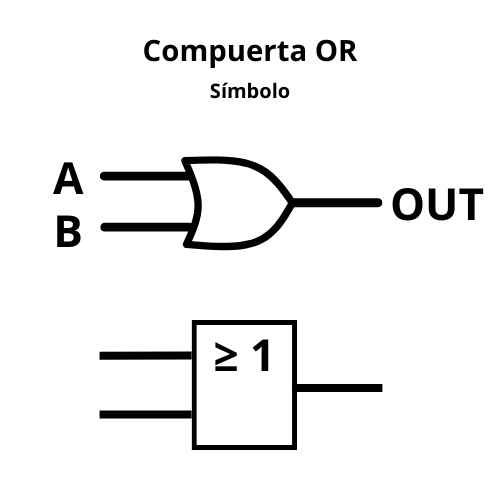
- OR (O)
- Función: La salida es 1 si al menos una entrada es 1.
- Símbolo: Rectángulo con “≥1” interno.
- Tabla de verdad compuerta lógica OR
| Entrada A | Entrada B | Salida (A OR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- NOT (NO)
- Función: Invierte la entrada (1 se convierte en 0 y viceversa).
- Símbolo: Triángulo con un círculo en la salida.
- Tabla de verdad compuerta lógica NOT
| Entrada A | Salida (NOT A) |
|---|---|
| 0 | 1 |
| 1 | 0 |

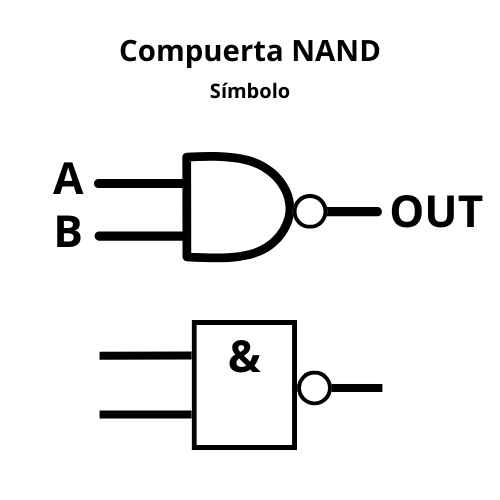
- NAND (NO-Y)
- Función: Es la combinación de AND y NOT. La salida es 0 solo si todas las entradas son 1.
- Dato clave: Es una compuerta universal, lo que significa que se puede usar para construir cualquier otro tipo de compuerta.
- Tabla de verdad compuerta lógica NAND
| Entrada A | Entrada B | Salida (A NAND B) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
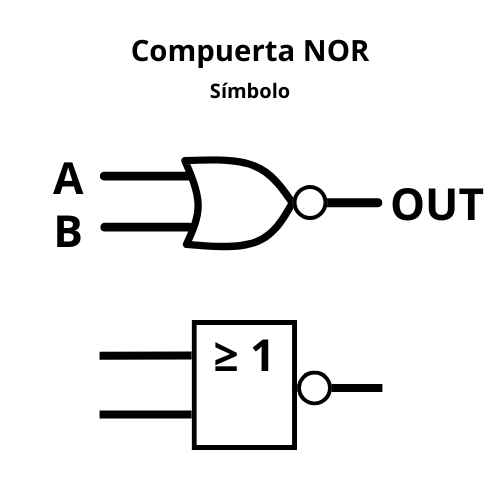
- NOR (NO-O)
- Función: Es la combinación de OR y NOT. La salida es 1 solo si todas las entradas son 0.
- Dato clave: También es universal, ideal para diseñar circuitos completos usando una sola familia de compuertas.
- Tabla de verdad compuerta lógica NOR
| Entrada A | Entrada B | Salida (A NOR B) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
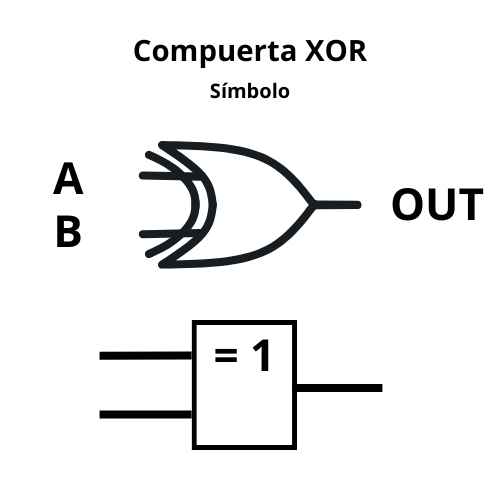
- XOR (O Exclusiva)
- Función: La salida es 1 si las entradas son diferentes.
- Analogía: Como decidir entre dos sabores: solo eliges uno, pero no ambos a la vez.
- Tabla de verdad compuerta lógica XOR
| Entrada A | Entrada B | Salida (A XOR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
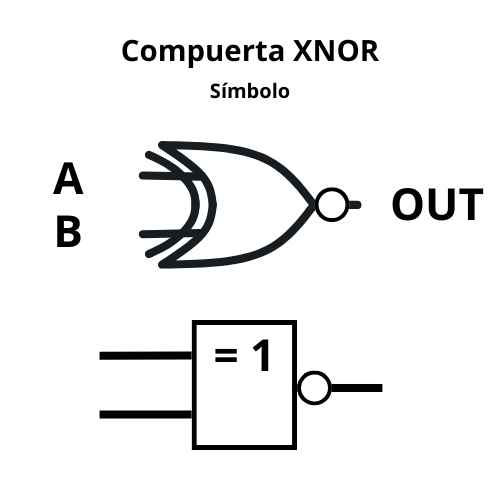
- XNOR (NO-O Exclusiva)
- Función: La salida es 1 si las entradas son iguales.
- Analogía: Imagina un espejo que refleja exactamente lo que tiene enfrente: solo produce “1” cuando ambas imágenes coinciden.
- Tabla de verdad compuerta lógica XNOR
| Entrada A | Entrada B | Salida (A XNOR B) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Álgebra Booleana: La Matemática Detrás de las Compuertas Lógicas
El álgebra booleana es el lenguaje matemático que usamos para describir el funcionamiento de las compuertas lógicas. Piensa en ella como la “receta” que indica qué ingredientes (entradas) necesitas para obtener el resultado deseado (salida).
En el álgebra booleana, los símbolos “+” y “·” tienen roles específicos y equivalentes a las operaciones OR y AND, respectivamente. Es decir, cuando usamos “A + B”, estamos indicando que la salida será 1 si al menos una de las entradas A o B es 1 (equivalente a la compuerta OR). Por otro lado, “A · B” (o simplemente A B) representa la operación AND, donde la salida será 1 solo si ambas entradas son 1. Puedes pensar en “+” como el botón que activa una alarma cuando cualquier sensor se dispara, mientras que “·” es como un candado que solo se abre cuando se cumplen todas las condiciones al mismo tiempo.
Además, en el álgebra booleana se utiliza el símbolo de negación, representado como A‾ (o A’ en otra notación). Este símbolo, ubicado en la parte superior derecha de la variable, indica su complemento: si A es 1, entonces A‾ es 0, y viceversa. Es como un interruptor que invierte el estado de la señal. Esta notación es fundamental para operaciones como la compuerta NOT y para simplificar funciones lógicas en el diseño de circuitos.
Algunas Leyes Básicas:
Ley de Identidad
- A + 0 = A
- A ⋅ 1 = A
Estas expresiones indican que sumar 0 o multiplicar por 1 no altera el valor de una variable, manteniendo la integridad de la señal.
Ley de Complemento
- A + A’ = 1
- A ⋅ A’ = 0
Una variable combinada con su complemento produce siempre el resultado máximo (1) en OR y el mínimo (0) en AND, lo que es clave para detectar estados opuestos.
Leyes de De Morgan
- (A + B)’ = A’ ⋅ B’
- (A ⋅ B)’ = A’ + B’
Estas reglas permiten transformar expresiones negadas en formas equivalentes, intercambiando operaciones AND y OR y negando las variables.
Ley Conmutativa
- A + B = B + A
- A ⋅ B = B ⋅ A
El orden de las variables no afecta el resultado, lo que permite reorganizar las expresiones para facilitar la simplificación.
Ley Asociativa
- A + (B + C) = (A + B) + C
- A ⋅ (B ⋅ C) = (A ⋅ B) ⋅ C
La forma en que se agrupan las variables en una operación OR o AND no cambia el resultado final, facilitando el manejo de múltiples términos.
Ley Distributiva
- A ⋅ (B + C) = (A ⋅ B) + (A ⋅ C)
- A + (B ⋅ C) = (A + B) ⋅ (A + C)
Esta ley permite “distribuir” una operación sobre otra, similar a la multiplicación en el álgebra clásica, y es fundamental para reconfigurar funciones lógicas.
Ley de Idempotencia
- A + A = A
- A ⋅ A = A
Repetir la misma variable en una operación OR o AND no altera su valor, lo que contribuye a eliminar redundancias en las expresiones.
Ley de Dominación
- A + 1 = 1
- A ⋅ 0 = 0
En una operación OR, la presencia del 1 domina el resultado, y en una operación AND, el 0 anula el resultado, definiendo límites claros en la lógica digital.
Ejemplos practicos álgebra booleana para compuertas lógicas
Ejemplo: Sistema de Iluminación Inteligente con Arduino con compuertas lógicas
Imagina que estás trabajando en un proyecto con Arduino y tienes dos sensores:
- Sensor de Movimiento (A): Detecta si hay alguien en la habitación (1 si detecta movimiento, 0 si no).
- Sensor de Luz Ambiental (B): Determina si el ambiente es oscuro (1 cuando está oscuro, 0 cuando hay suficiente luz).
Quieres que una lámpara se encienda solo cuando se detecte movimiento y la habitación esté oscura. Usando álgebra booleana, puedes expresar esta condición con la función:
F = A ⋅ B
Esto significa que la lámpara (F) se activará (F = 1) únicamente cuando:
- El sensor de movimiento detecta presencia (A = 1)
- Y el sensor de luz confirma que el ambiente es oscuro (B = 1)
Si alguna de estas condiciones falla, por ejemplo, si no hay movimiento (A = 0) o si la habitación ya está iluminada (B = 0), la función F dará como resultado 0 y la lámpara se mantendrá apagada.
Es como tener un “guardián digital” que solo despierta y enciende la luz cuando ambas condiciones son ideales. Este ejemplo demuestra de forma práctica cómo el álgebra booleana y las compuertas lógicas se utilizan para tomar decisiones en sistemas electrónicos reales.
Ejemplo: Alarma de Inactividad
Imagina que necesitas un sistema de alarma para una zona donde siempre debe haber actividad (por ejemplo, una sala de servidores o un área de vigilancia). La alarma debe activarse solo cuando no haya movimiento y la puerta esté cerrada, indicando que algo no está funcionando correctamente.
Para esto, empleamos dos sensores:
- Sensor de Puerta (P): Registra 1 si la puerta está abierta y 0 si está cerrada.
- Sensor de Movimiento (M): Registra 1 si se detecta movimiento y 0 si no lo hay.
El objetivo es que la alarma se active solo cuando la puerta esté cerrada (P = 0) y no haya movimiento (M = 0).
Para lograrlo, usamos una compuerta NOR, cuya función es:Alarma=¬(P+M)\text{Alarma} = \neg (P + M)Alarma=¬(P+M)
Esto significa que la salida será 1 solo cuando ambas entradas sean 0, es decir, cuando la puerta esté cerrada y no haya movimiento.
| P (Puerta) | M (Movimiento) | NOR (Alarma) |
|---|---|---|
| 0 (Cerrada) | 0 (Sin movimiento) | 1 (Alarma encendida) |
| 0 (Cerrada) | 1 (Movimiento) | 0 (Alarma apagada) |
| 1 (Abierta) | 0 (Sin movimiento) | 0 (Alarma apagada) |
| 1 (Abierta) | 1 (Movimiento) | 0 (Alarma apagada) |
Así, la alarma solo se activará cuando no haya movimiento y la puerta esté cerrada.
Modelos comerciales de las compuertas lógicas
A continuación, te presentamos una clasificación práctica de las compuertas lógicas más relevantes, junto con su «matrícula comercial» (número de circuito integrado), para que puedas identificar rápidamente qué componente usar en tus proyectos. Ideal para estudiantes, ingenieros y makers que buscan un puente claro entre la teoría y la práctica.
Compuertas Básicas
Las compuertas básicas son los bloques fundamentales de la electrónica digital. Realizan operaciones lógicas simples como AND, OR, NOT, NAND, NOR, XOR y XNOR, y son esenciales para construir circuitos más complejos.
- 74LS00: Compuerta NAND (2 entradas).
- 74LS02: Compuerta NOR (2 entradas).
- 74LS04: Compuerta NOT (Inversor, 1 entrada).
- 74LS08: Compuerta AND (2 entradas).
- 74LS32: Compuerta OR (2 entradas).
- 74LS86: Compuerta XOR (2 entradas).
- 74LS266: Compuerta XNOR (2 entradas).
Compuertas con Más Entradas
Estas compuertas permiten manejar tres o más entradas, lo que las hace ideales para circuitos que requieren lógica más compleja o múltiples condiciones.
- 74LS10: Compuerta NAND (3 entradas).
- 74LS11: Compuerta AND (3 entradas).
- 74LS20: Compuerta NAND (4 entradas).
- 74LS21: Compuerta AND (4 entradas).
- 74LS27: Compuerta NOR (3 entradas).
- 74LS4002: Compuerta NOR (4 entradas).
Compuertas con Funcionalidades Especiales
Estas compuertas están diseñadas para aplicaciones específicas, como mejorar la inmunidad al ruido, combinar múltiples operaciones lógicas o manejar entradas complejas.
- 74LS51: Compuerta AND-OR-Invert (Combinación de AND, OR y NOT).
- 74LS132: Compuerta NAND con disparo Schmitt (2 entradas, mejora la inmunidad al ruido).
- 74LS135: Compuerta XOR (3 entradas).
Circuitos Integrados Relacionados
Aunque no son compuertas lógicas, estos circuitos integrados son complementarios y amplían las funcionalidades de los sistemas digitales, como la transferencia de datos, la comparación de señales o el control de displays.
- 74LS47: Decodificador BCD a 7 segmentos (Para displays).
- 74LS83: Sumador binario de 4 bits.
- 74LS85: Comparador de 4 bits.
- 74LS138: Demultiplexor 1:8.
- 74LS151: Multiplexor 8:1.
- 74LS244: Buffer octal (Amplificador de señal).
- 74LS245: Octal Transceptor de Bus (Transferencia bidireccional de datos).
La correcta selección y aplicación de estas compuertas y circuitos integrados son fundamentales para lograr el rendimiento y la eficiencia deseados en proyectos electrónicos. Su versatilidad y amplia disponibilidad facilitan su integración en diversas aplicaciones tecnológicas.
Aplicaciones en Electrónica Digital
Las compuertas lógicas no son solo teoría; tienen aplicaciones muy prácticas, como:
- Circuitos combinacionales: Decodificadores, multiplexores y sumadores que se usan en CPUs.
- Sistemas de control: Como los semáforos o alarmas, donde cada sensor actúa como una entrada.
- Procesamiento de datos: Fundamentales en la operación de computadoras y dispositivos IoT.
Proyectos Prácticos con Compuertas Lógicas 🛠️
Proyecto 1: Alarma Anti-intrusos con Sensor y Compuerta AND
Materiales:
- Sensor infrarrojo (ej. KY-032)
- Compuerta AND (IC 7408)
- Zumbador y fuente de 5V
Funcionamiento:
El zumbador se activa solo si el sensor detecta movimiento y el sistema está armado. Es como un “candado digital” que solo se abre cuando se cumplen todas las condiciones.
Proyecto 2: Simulador de Compuertas con Arduino
Utiliza el IDE de Arduino para programar compuertas lógicas virtuales y probar diferentes tablas de verdad.
Analogía: Es como un videojuego de simulación donde puedes experimentar con tus propios circuitos sin necesidad de soldar componentes reales.
Preguntas Frecuentes
- ¿Qué compuertas se usan en sistemas modernos?
Las compuertas NAND y NOR son muy populares debido a su versatilidad y capacidad para construir otros tipos de compuertas. - ¿Cómo representar una función booleana con compuertas?
Escribe la tabla de verdad, obtén la ecuación simplificada (usando mapas de Karnaugh) e implementa la función con compuertas universales. - ¿Existen compuertas con más de dos entradas?
¡Sí! Por ejemplo, una AND de 3 entradas activa su salida solo si todas son 1, ideal para circuitos que requieren múltiples condiciones.
Simulador compuertas lógicas
Esta herramienta interactiva te permite explorar y comprender el funcionamiento de las principales compuertas lógicas utilizadas en electrónica digital, como AND, OR, NOT, NAND, NOR y XOR.
¿Cómo utilizar el simulador?
Información adicional: Se proporciona el número del circuito integrado (IC) asociado a la compuerta seleccionada para un contexto más amplio.
Selecciona la compuerta lógica: Utiliza el menú desplegable para elegir la compuerta que deseas simular.
Define el número de entradas: Para compuertas con múltiples entradas, selecciona la cantidad (2 o 3) según tu interés.
Configura las entradas: Activa o desactiva las entradas utilizando las casillas de verificación correspondientes.
Observa la salida: El simulador mostrará el resultado de la operación lógica basada en las entradas seleccionadas.
Simulador de Compuertas Lógicas
Conclusión: ¡Lleva la Teoría a la Práctica!
Las compuertas lógicas son el ABC de la electrónica digital. Conocer su funcionamiento y aplicaciones te permite diseñar desde simples circuitos de control hasta complejos sistemas de procesamiento de datos. ¿Listo para crear tu primer proyecto? ¡Comparte tus resultados en redes y únete a la comunidad de makers en México!
Documentación y ligas externas
Wikipedia: Puerta Lógica
Video: Compuertas lógicas, ¿Qué son y dónde se utilizan?





